Modelleringsoppgave II#
I dette prosjektet skal dere modellere en naturvitenskapelig sammenheng ved å bruke differensiallikninger. Prosjektet skal presenteres på en ryddig måte med teori, programkode og drøfting i Jupyter Notebook. Oppgavene er ment som en veiledning til momenter dere bør ha med, men rapporten skal ikke struktureres etter oppgavene. Alle oppgaver og sentrale momenter skal være en integrert del av en helhetlig rapport. Dere vil bli vurdert etter følgende kriterier:
Koden virker og er lagt opp på en god måte.
Koden er strukturert og oversiktlig.
Det kommer fram at dere kan anvende grunnleggende programmering på en hensiktsmessig måte.
Det kommer fram at dere forstår det realfaglige innholdet.
Modellene som er brukt, er differensiallikninger.
Rapporten er ryddig og oversiktlig. Rapporten skal ikke være inndelt etter oppgaver, men ha en klar struktur:
Introduksjon: Hva dreier prosjektet seg om. Hva skal du vise/gjøre?
Hvilke metoder bruker du? Utled metodene.
Beskrivelse, resultater og drøfting: Gjør rede for framgangsmåte og programmer. Drøft de ulike modellene: Begrensninger, forutsetninger, antakelser, konsekvenser. Hva innebærer en endring av de ulike parametrene?
Konklusjon: Hva har du gjort, og hvordan? Kort oppsummering.
Alle figurer og grafer er oversiktlige med figurtekst, aksetitler o.l.
Alle resultater er drøfta og redegjort for.
Oppgaver#
Velg én av oppgavene nedenfor, eller foreslå en problemstilling for læreren. Problemstillingen må bli godkjent før dere går i gang med prosjektet.
Oppgave 1: Zombie-apokalypse (biologi)#
Denne oppgava tar utgangspunkt i å modellere og simulere en menneskepopulasjon under en zombie-apokalypse. Gjør rede for begrensninger for modellene dine, og drøft hva de forteller oss om populasjonen.
Utgangspunkt#
Vi befinner oss i en postapokalyptisk situasjon der verden har blitt utsatt for et virus som gjør mennesker om til zombier. Viruset smitter kun via blod, f.eks. ved bitt eller kloring fra zombier. Vi skal studere en avsideliggende landsby, Alexandria, som ligger i nærheten av Washington D.C., og som etter et zombie-utbrudd har blitt et tilfluktssted for 500 mennesker. De har tilgang til en del mat og våpen, og de har en mur rundt hele landsbyen som holder zombiene unna. Men de må også ut for å finne nye ressurser og andre mennesker som trenger hjelp, så de er aldri helt trygge.
Oppgave#
Modellen din kan inneholde mange ulike faktorer, og du står fritt til å legge til flere, dersom du begrunner det. Legg til én og én faktor, og test modellen etter hver gang. Kommenter populasjonsutviklinga etter hver nye faktor er lagt til. Her er et forslag til framgangsmåte:
Lag først et program der menneskene er trygge mot zombier, og der nye mennesker kan komme til ved fødsel og (mer sannsynlig) innvandring. Lag gjerne ett ledd i likninga som inkluderer begge disse faktorene.
Legg inn en ressursbegrensning (bæreevne) for populasjonen. Hvilke faktorer påvirker denne?
Menneskene kan også dø av sykdom, skade og alderdom (naturlig død). Legg dette inn i modellen, og tenk på hvor sannsynlig dette er (hvor god er tilgangen på medisiner, lege o.l.?).
Nå skal du legge inn en zombiepopulasjon som lever i nærheten av Alexandria. Du kan selv bestemme hvor mange zombier som finnes og hvor sannsynlig det er at mennesker blir drept av en zombie. Zombiene fungerer som rovdyr, slik at menneskene ikke blir til zombier i denne modellen.
Nå kan du legge inn muligheten for at mennesker blir til zombier hvis de blir bitt, men ikke revet i fillebiter. Det vil si at noen mennesker vil bli smitta, mens andre vil bli drept av zombiene. De som blir smitta, blir til zombier, og dermed øker zombiepopulasjonen.
Alexandria kan slå tilbake mot zombiene. Legg inn en faktor som bidrar til at menneskene kan ta livet av zombier.
I nærheten av Alexandria finner vi landsbyene Hilltop og Kingdom. Fra disse kan det komme forsterkninger til Alexandria ved behov. Inkluder dette i modellen din.
Oppgave 2: Klimamodell 1 – Ozonlaget (kjemi)#
Vi kan også simulere kjemiske reaksjoner ved hjelp av modeller for reaksjonsfart. Disse modellene lar oss forutsi hvordan og hvor fort en kjemisk reaksjon vil gå. Dette kan brukes til å simulere alt fra industrielle prosesser til viktige reaksjoner i miljøet. Her skal vi se på modeller som kan forutsi hvordan det vil gå med ozonlaget i framtida.
Farstlover#
Modeller for reaksjonsfart kaller vi fartslover. En fartslov beskriver endringen i konsentrasjon i en kjemisk reaksjon. La oss ta et enkelt eksempel der vi har to reaktanter og ett produkt:
Fartsloven for denne reaksjonen må bestemmes eksperimentelt, og er derfor en empirisk lov. For eksempel kan endringen i konsentrasjonen til C være gitt ved:
Her betyr \(\frac{d[C]}{dt}\) den deriverte av [C] med hensyn på tid (c’(t)). Det vil si at endringen i konsentrasjonen til produktet C er avhengig av konsentrasjonen til begge reaktanter i like stor grad. Men det kunne jo være at endringen i [C] varierte mer med [A] enn med [B], eller for eksempel ikke med [A] i det hele tatt. Da kunne vi henholdsvis fått disse modellene:
Eksperimenter avgjør hvilken form vi gir fartslovene. Og dersom endringen av [C] er gitt ved \(\frac{d[C]}{dt} = k[A][B]\), kan vi ut fra reaksjonslikningen utlede følgende sammenhenger (forklar hvorfor!):
Fartslover for dannelse og nedbrytning av ozon i stratosfæren#
Den såkalte Chapman-modellen kan benyttes for å simulere produksjon og nedbrytning av ozon i stratosfæren. Den er basert på følgende reaksjonslikninger med tilhørende reaksjonskoeffisienter:
hvor O, O\(_2\) og O\(_3\) er henholdsvis oksygen, dioksygen og ozon. M er en ikke-reagerende støtpartner, mens \(h \nu\) og \(h \nu '\) er energi tilført av UV-stråling med bølgelengde, \(\lambda\), under 242 nm og 336 nm, henholdsvis.
Den første reaksjonslikningen beskriver spaltingen av O\(_2\) til 2 O-atomer som resultat av UV-stråling. Den andre reaksjonslikningen viser den påfølgende reaksjonen mellom O\(_2\) og O som krever en kollisjon med M for å danne O\(_3\), mens de to siste reaksjonslikningene viser hvordan O\(_3\) brytes ned henholdsvis som resultat av UV-stråling for å danne O og O\(_2\), og gjennom reaksjon med O for produksjon av 2 O\(_2\)-molekyler.
Fartslovene for [O], [O\(_2\)] og [O\(_3\)] er gitt ved henholdsvis
Ratekonstantene er gitt som følger:
Ratekonstantene er gitt ved omtrent 25 km høyde, hvor \([\textrm{M}] \approx 9.0 \times 10^{17}\) molekyler cm\(^{-3}\). Systemet har følgende initialbetingelser:
Oppgaver#
a) Lag et program som beregner og plotter [O\(_3\)] og [O] som funksjon av tid i intervallet \(t \in [0,100]\) ved å benytte Forward Euler-algoritmen på fartslovene i teoridelen med de gitte initialbetingelsene og tidssteg \(h = 0.001\). Plott med logaritmisk skala på \(y\)-aksen (plt.yscale(‘log’)).
b) Beregn og plott de samme verdiene med en backward-metode (‘BDF) ved å bruke funksjonen scipy.integrate.solve_ivp fra Scipy-biblioteket for \(t \in [0,10^8]\). Evaluer punktene for t = np.linspace(t0,tid_slutt,int(1E6)).
c) Legg til justeringer i modellen eller søk og finn andre modeller du kan bruke. Ideer til endringer kan være å innkludere et økt utslipp av KFK-gasser (begrunn eventuelt hvorfor) og sammenlikninger av modellen med data og med andre modeller på internett.
Oppgave 3: Klimamodell II – Drivhuseffekten (fysikk)#
Det som hovedsakelig varmer opp planeten vår, er sollys. Sola sender ut energi i form av elektromagnetisk stråling som treffer jordkloden. All elektromagnetisk stråling som treffer toppen av atmosfæren, har blitt målt til ca 1361 kW/m\(^2\) Hvor mye energi som treffer toppen av atmosfæren er nesten konstant, og har bare variert med 0.2 prosent på 400 år. Strålingen blir kalt for solkonstanten (K\(_s\)).
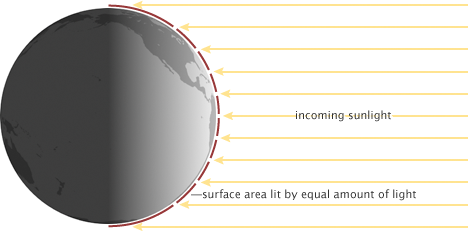
Energien som treffer planeten kan beregnes slik:
a) Forklar hva vi forutsetter om modellen vår dersom vi bruker uttrykket ovenfor til å beregne hvor mye energi som treffer jorda.
Ikke all energi som treffer jorda, blir absorbert av jordas overflate. En del energi reflekteres tilbake på grunn av jordas albedo. Den absorberte energien kan beregnes slik:
b) Forklar hvorfor vi kan uttrykke den absorberte energien som ovenfor. c) Beregn energien som treffer jorda, og energien som jorda absorberer. Hvor mange prosent blir absorbert?
Alle legemer sender også ut (emitterer) energi. Dette kan beskrives med Stefan-Boltzmann-loven:
\(\sigma\) er Stefan-Boltzmann constant. \(\sigma = 5.670373 \cdot 10^{-8} W / (m^2K^4)\)
På grunn av energiprinsippet, loven om at energi er konstant, må energi inn på planeten være det samme som energi ut. Da har vi at:
d) Bruk dette energiprinsippet og uttrykkene ovenfor til å finne et uttrykk for den gjennomsnittlige temperaturen til jordkloden. Kommenter svaret og forklar hvilken modell du nå har brukt.
Modellen vi nå har brukt, tar ikke hensyn til atmosfæren. Når vi legger til atmosfæren, kan vi først gjøre følgende forenklinger:
Atmosfæren har en konstant temperatur. Det vil si at vi modeller atmosfæren som en stor blokk hvor hele blokken har den samme temperaturen.
Atmosfæren er fullstendig gjennomsiktig for stråling fra sola. Det vil si at all stråling fra sola treffer jordoverflaten.
Atmosfæren tar imot all strålinga fra jorden.
e) Legg til atmosfæren i modellen din. Du må fortsatt bruke energibevaring som utgangspunkt, men beregne energi inn og ut av atmosfæren hver for seg. Da får du to likninger som du kan kombinere for å få en løsning or temperaturen.
f) Nå kan du legge til flere faktorer i modellen din, f.eks. flere lag i atmosfæren. Her kan du lage modeller selv, eller du kan søke opp informasjon om ulike klimamodeller. Finn temperaturen for hver modell, og drøft modellene og resultatene underveis.
Oppgave 4: Solsystemet (fysikk)#
Solsystemet har lenge vært til fascinasjon og undring for mennesker. Selv i et så stort system som solsystemet kan en simulere planetenes baner med god tilnærming ved å kun bruke Newtons lover!
Teoretisk bakgrunn#
Hvis vi ser på kraften som virker mellom to planeter, en med masse \(m_1\) og én med masse \(m_2\), kan vi bruke Newtons universelle gravitasjonslov. Loven forteller oss at for to legemer med masse \(m_1\) og \(m_2\) som kan ansees å ha perfekt kuleform, er kraften mellom dem \(F = \frac{Gm_1m_2}{r^2}\). Vi bruker denne loven til å finne kreftene som virker på dem. Vi kan anta at planetene beveger seg i to dimensjoner, det vil si langs \(x\)- og \(y\)-aksen. Hvis du vil ha en mer realistisk simulering ved å inkludere en tredje dimensjon, dvs. \(z\)-aksen, er det mulig å utvide modellen med å gjøre akkurat det samme for \(z\)-aksen som modellen har gjort for \(x\)- og \(y\)-aksen, men dette er valgfritt. Kraften som virker på en planet med masse \(m_1\) langs \(x\)- og \(y\)-aksen, \(F_{x}\) og \(F_{y}\), blir påvirka av en planet med masse \(m_2\). Kreftene langs \(x\)- og \(y\)-aksen kan uttrykkes ved:
der \(G\) er gravitasjonskonstanten, \(r\) er avstanden mellom planetene og \(x(t)\) og \(y(t)\) er posisjonen til planeten med masse \(m_1\) langs henholdsvis \(x\)- og \(y\)-aksen etter ei tid \(t\). Vi har også at \(x_2(t)\) og \(y_2(t)\) er posisjonen til planeten med masse \(m_2\) langs henholdsvis \(x\)- og \(y\)-aksen etter ei tid \(t\).
Oppgaver#
Vis at akselerasjonen \(a_{x}(t)\) og \(a_y(t)\) til en planet med masse \(m_1\) langs henholdsvis \(x\)- og \(y\)-aksen er:
\[a_x(t) = -\frac{G\cdot m_2\cdot x(t)}{r^3}\]\[a_y(t) = -\frac{G\cdot m_2\cdot y(t)}{r^3}\]Forklar hvorfor vi får at disse likningene må løses for å finne posisjonene \(x(t)\) og \(y(t)\):
\[x'(t) = v_x(t)\]\[y'(t) = v_y(t)\]\[v_x'(t) = -\frac{G\cdot m_2\cdot x(t)}{r^3}\]\[v_y'(t) = -\frac{G\cdot m_2\cdot y(t)}{r^3}\]der \(v_x(t)\) og \(v_y(t)\) er farten til planeten med masse \(m_1\).
Nå skal vi se på et solsystem som består av kun jorda og sola. Modellen antar at sola står stille. Du kan derfor fokusere på hvordan jordas bane blir påvirket av sola.
I denne modellen lar vi jordas masse \(m_1 = 3\cdot 10^{-6}\) solmasser og solas masse \(m_2 = 1\) solmasse. Solmasser er en enhet som forteller stor en planet er i forhold til sola. Ved å bruke AU (enhet brukt som den gjennomsnittlige avstanden mellom sol og jord) og år som enheter i vår modell, kan vi finne at \(G = 4\pi^2\).
La startbetingelsene til jorda være \(x(0) = 1\), \(y(0) = 0\), \(v_x(0) = 0\) og \(v_y(0) = 2\pi\). Sola kan stå i origo. Det betyr at i dette tilfellet vil \(x_2(t) = 0\) og \(y_2(t) = 0\) for alle tider \(t\).
Skriv et program som først bruker Eulers metode til å finne jordas bane rundt sola for ett år ved å bruke \(N = 1000\) tidssteg. La programmet plotte banen.
Euler-Cromers metode er en liten justering av Eulers metode. Finn ut hva som menes med denne metoden. Skriv om programmet fra deloppgave c) slik at det bruker Euler-Cromer isteden med samme verdi for \(N\). Hvordan er plottet nå, sammenlikna med plottet fra deloppgave c)?
Men vi kan jo ikke ha bare én planet i solsystemet vårt! Nå skal vi se på hvordan simuleringa kan være dersom vi har med flere planeter i solsystemet. Merk at \(x_2(t)\) og \(y_2(t)\) nå vil være avhengig av hvilken planet vi ser på. Du kan fortsatt anta at sola står stille.
Skriv et program som modellerer planetenes bane for \(P\) planeter. Du kan gjerne bruke fila planetermalstruktur.py som forslag til programstruktur i programmet ditt, men du kan også utvide programmet ditt fra d). Hvis du skriver om programmet ditt fra d), er det viktig at det greier å lese en datafil med info over planetenes startposisjon, startfart og masse.
Forslaget til programstrukturen henter ut eksempeldata fra ei fil som heter planeter_data.dat. Tallene er henta fra NASA og har blitt noe modifisert. Du kan finne sida her: https://ssd.jpl.nasa.gov/horizons.cgi. Sola er ikke tatt med, da simuleringa antar at den står i origo og ikke beveger seg.
Kommentar til struktur:
Vi har ikke jobba så mye med matrisestrukturer. Tankegangen bak strukturen til pos og fart i planetermalstruktur.py kan illustreres slik:
Illustrasjon viser tankegangen bak pos, som er helt den samme for fart. Her kan en tenke at vi lagrer informasjonen over planetene i et arkiv. Det \(j\)-te “arket” med informasjon til den \(j\)-te planeten hentes ut ved pos[:,:,\(j\)]. Skal vi se hvor den \(j\)-te planeten befinner seg langs både \(x\)- og \(y\)-aksen ved et tidssteg \(i\), bruker vi pos[\(i\),:,\(j\)]. Skal vi for eksempel bare se på \(x\)-verdien til den \(j\)-te planeten ved tidssteg \(i\), bruker vi pos[\(i\),0,\(j\)], og 1 istedenfor 0 dersom vi skal se på \(y\)-verdien.
Du kan sjekke om simuleringa di gir følgende planetbaner etter ett år ved å bruke informasjonen fra fil planeter_data.dat. Fildataene gir følgende resultater av simuleringa etter ett år:
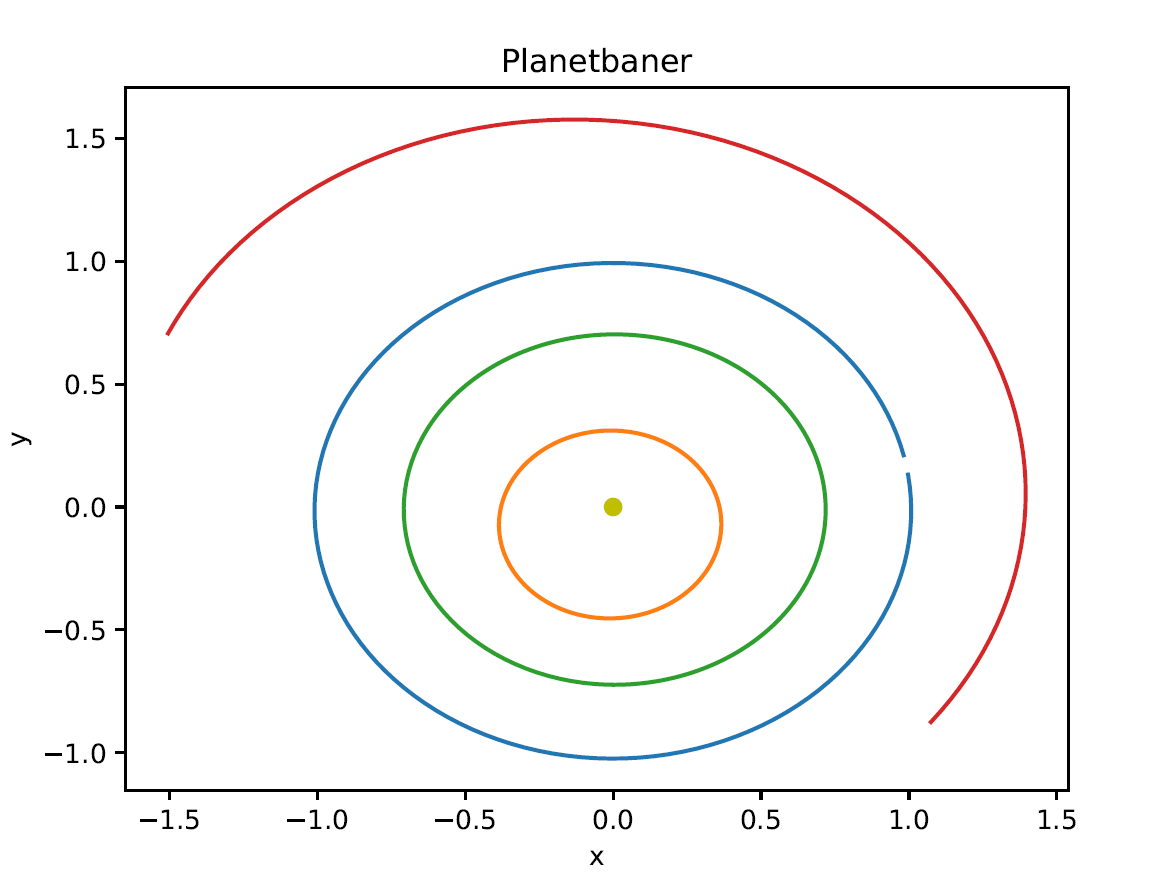
Bruk pygame til å visualisere planetenes bane rundt sola. Du får et forslag til hvordan programstrukturen kan være, men utvid gjerne med mer om du har lyst. Her er det kun fantasien som setter grenser! Et forslag til programstruktur har filnavnet planetermalpygame.py.